
Department of Systems and Mathematical Science
|
■シークエント計算 |
シークエント計算は、数理論理学の正しい文から正しい文を導き出す形式的操作の一つです。 これにもとづいて、数学に関するある種類の証明を系統的に行うことができます。
下記の図は、集合の包含関係の推移性、すなわち、
「任意の集合X,Y,Zに対して、X⊂YかつY⊂Zならば、X⊂Z」
のシークエント計算にもとづいた証明です。
これを証明図とよびます。
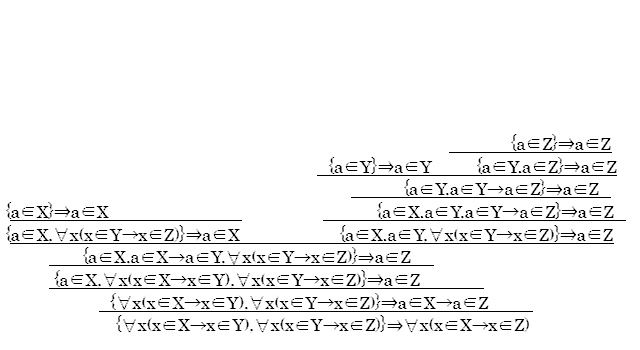
証明図における文と文の関係は、「上から下が導かれる」と解釈します。 一番上には「{a∈X}⇒a∈X」の形の表現がありますが、 これは「aがXの要素ならば、aがXの要素である」を意味します。 この文は明らかに正しいといえるでしょう。 一番下の表現は、少し複雑ですが、 証明の目的である「任意の集合X,Y,Zに対して、X⊂YかつY⊂Zならば、X⊂Z」を意味します。 このように、証明図は、明らかに正しい文の表現からはじめて、下に向かってより複雑な表現を導き、 一番下に目的の表現を導く形をとります。
webmaster@ss.nanzan-u.ac.jp