Department of Systems and Mathematical Science

システム数理学科トップ＞背景画像説明＞主成分分析

■主成分分析

主成分分析とは統計学における主要な方法の一つです。 その方法を簡単に説明すると、変数の多いデータに対して少ない次元でその構造を解き明かす統計的方法と言えます。

下記の図は各都道府県に住む人の1日の中での時間の使い方（睡眠とか食事とか16個の変数からなる） について主成分分析をかけたものです。 主成分分析ではその少ない次元（それを主成分と呼びます）に対して どのような変数が聞いているかをまず考えますが、 ここではそのもとで得られるデータのプロット図の方を示しました。

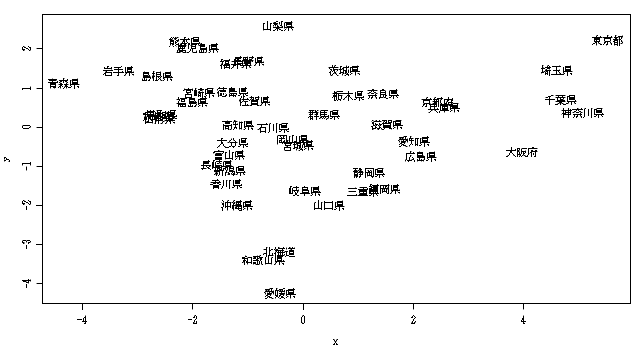
ここでは元の変数の影響について説明しましょう。

横方向が第1主成分と呼ばれるもので、 正の方向には「通勤」や「買い物」、負の方向には「睡眠」や「休養」が 効いています。そのため、忙しい毎日を送っているかゆったりした毎日を送っているかの違いになります。 忙しい方に大都会が集まっているのが分かります。

縦方向が第2主成分と呼ばれるもので、 正の方向には「食事」・「仕事」・「学業」、負の方向には「TV」や「趣味」が 効いています。そのため、勤勉な生活を送っているか趣味中心の生活を送っているかの違いになります。 この分類では都会や田舎という単純な構造ではなく面白い結果になっています。